4th Dimension v3.5.1 serial key or number

4.10.

4.10.1. Introduction

This section is non-normative.

A form is a component of a Web page that has form controls, such as text fields, buttons, checkboxes, range controls, or color pickers. A user can interact with such a form, providing data that can then be sent to the server for further processing (e.g., returning the results of a search or calculation). No client-side scripting is needed in many cases, though an API is available so that scripts can augment the user experience or use forms for purposes other than submitting data to a server.

Writing a form consists of several steps, which can be performed in any order: writing the user interface, implementing the server-side processing, and configuring the user interface to communicate with the server.

4.10.1.1. Writing a form’s user interface

This section is non-normative.

For the purposes of this brief introduction, we will create a pizza ordering form.

Any form starts with a element, inside which are placed the controls. Most controls are represented by the element, which by default provides a one-line text field. To label a control, the element is used; the label text and the control itself go inside the element. Each area within a form is typically represented using a element. Putting this together, here is how one might ask for the customer’s name:

To let the user select the size of the pizza, we can use a set of radio buttons. Radio buttons also use the element, this time with a attribute with the value . To make the radio buttons work as a group, they are given a common name using the attribute. To group a batch of controls together, such as, in this case, the radio buttons, one can use the element. The title of such a group of controls is given by the first element in the , which has to be a element.

Changes from the previous step are highlighted.

To pick toppings, we can use checkboxes. These use the element with a attribute with the value :

The pizzeria for which this form is being written is always making mistakes, so it needs a way to contact the customer. For this purpose, we can use form controls specifically for telephone numbers ( elements with their attribute set to ) and e-mail addresses ( elements with their attribute set to ):

We can use an element with its attribute set to to ask for a delivery time. Many of these form controls have attributes to control exactly what values can be specified; in this case, three attributes of particular interest are , , and . These set the minimum time, the maximum time, and the interval between allowed values (in seconds). This pizzeria only delivers between 11am and 9pm, and doesn’t promise anything better than 15 minute increments, which we can mark up as follows:

The element can be used to provide a free-form text field. In this instance, we are going to use it to provide a space for the customer to give delivery instructions:

Finally, to make the form submittable we use the element:

4.10.1.2. Implementing the server-side processing for a form

This section is non-normative.

The exact details for writing a server-side processor are out of scope for this specification. For the purposes of this introduction, we will assume that the script at is configured to accept submissions using the format, expecting the following parameters sent in an HTTP POST body:

Customer’s name

Customer’s telephone number

Customer’s e-mail address

The pizza size, either , , or

A topping, specified once for each selected topping, with the allowed values being , , , and

The requested delivery time

The delivery instructions

4.10.1.3. Configuring a form to communicate with a server

This section is non-normative.

Form submissions are exposed to servers in a variety of ways, most commonly as HTTP GET or POST requests. To specify the exact method used, the attribute is specified on the element. This doesn’t specify how the form data is encoded, though; to specify that, you use the attribute. You also have to specify the URL of the service that will handle the submitted data, using the attribute.

For each form control you want submitted, you then have to give a name that will be used to refer to the data in the submission. We already specified the name for the group of radio buttons; the same attribute () also specifies the submission name. Radio buttons can be distinguished from each other in the submission by giving them different values, using the attribute.

Multiple controls can have the same name; for example, here we give all the checkboxes the same name, and the server distinguishes which checkbox was checked by seeing which values are submitted with that name — like the radio buttons, they are also given unique values with the attribute.

Given the settings in the previous section, this all becomes:

There is no particular significance to the way some of the attributes have their values quoted and others don’t. The HTML syntax allows a variety of equally valid ways to specify attributes, as discussed in §8 The HTML syntax.

For example, if the customer entered "Denise Lawrence" as their name, "555-321-8642" as their telephone number, did not specify an e-mail address, asked for a medium-sized pizza, selected the Extra Cheese and Mushroom toppings, entered a delivery time of 7pm, and left the delivery instructions text field blank, the user agent would submit the following to the online Web service:

4.10.1.4. Client-side form validation

This section is non-normative.

Forms can be annotated in such a way that the user agent will check the user’s input before the form is submitted. The server still has to verify the input is valid (since hostile users can easily bypass the form validation), but it allows the user to avoid the wait incurred by having the server be the sole checker of the user’s input.

The simplest annotation is the attribute, which can be specified on elements to indicate that the form is not to be submitted until a value is given. By adding this attribute to the customer name, pizza size, and delivery time fields, we allow the user agent to notify the user when the user submits the form without filling in those fields:

It is also possible to limit the length of the input, using the attribute. By adding this to the element, we can limit users to 1000 characters, preventing them from writing huge essays to the busy delivery drivers instead of staying focused and to the point:

When a form is submitted, events are fired at each form control that is invalid, and then at the element itself. This can be useful for displaying a summary of the problems with the form, since typically the browser itself will only report one problem at a time.

4.10.1.5. Enabling client-side automatic filling of form controls

This section is non-normative.

Some browsers attempt to aid the user by automatically filling form controls rather than having the user reenter their information each time. For example, a field asking for the user’s telephone number can be automatically filled with the user’s phone number.

To help the user agent with this, the attribute can be used to describe the field’s purpose. In the case of this form, we have three fields that can be usefully annotated in this way: the information about who the pizza is to be delivered to. Adding this information looks like this:

In physics, spacetime is any mathematical model which fuses the three dimensions of space and the one dimension of time into a single four-dimensionalmanifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive where and when events occur differently.

Until the 20th century, it was assumed that the 3-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. However, in 1905, Albert Einstein based a work on special relativity on two postulates:

• The laws of physics are invariant (i.e., identical) in all inertial systems (i.e., non-accelerating frames of reference)
• The speed of light in a vacuum is the same for all observers, regardless of the motion of the light source.

The logical consequence of taking these postulates together is the inseparable joining together of the four dimensions—hitherto assumed as independent—of space and time. Many counterintuitive consequences emerge: in addition to being independent of the motion of the light source, the speed of light is of constant magnitude regardless of the frame of reference in which it is measured; the distances and even temporal ordering of pairs of events change when measured in different inertial frames of reference (this is the relativity of simultaneity); and the linear additivity of velocities no longer holds true.

Einstein framed his theory in terms of kinematics (the study of moving bodies). His theory was an advance over Lorentz's 1904 theory of electromagnetic phenomena and Poincaré's electrodynamic theory. Although these theories included equations identical to those that Einstein introduced (i.e., the Lorentz transformation), they were essentially ad hoc models proposed to explain the results of various experiments—including the famous Michelson–Morley interferometer experiment—that were extremely difficult to fit into existing paradigms.

In 1908, Hermann Minkowski—once one of the math professors of a young Einstein in Zürich—presented a geometric interpretation of special relativity that fused time and the three spatial dimensions of space into a single four-dimensional continuum now known as Minkowski space. A key feature of this interpretation is the formal definition of the spacetime interval. Although measurements of distance and time between events differ for measurements made in different reference frames, the spacetime interval is independent of the inertial frame of reference in which they are recorded.^[1]

Minkowski's geometric interpretation of relativity was to prove vital to Einstein's development of his 1915 general theory of relativity, wherein he showed how mass and energycurve flat spacetime into a pseudo-Riemannian manifold.

Introduction[edit]

Definitions[edit]

Non-relativistic classical mechanics treats time as a universal quantity of measurement which is uniform throughout space, and separate from space. Classical mechanics assumes that time has a constant rate of passage, independent of the observer's state of motion, or anything external.^[2] Furthermore, it assumes that space is Euclidean; it assumes that space follows the geometry of common sense.^[3]

In the context of special relativity, time cannot be separated from the three dimensions of space, because the observed rate at which time passes for an object depends on the object's velocity relative to the observer. General relativity also provides an explanation of how gravitational fields can slow the passage of time for an object as seen by an observer outside the field.

In ordinary space, a position is specified by three numbers, known as dimensions. In the Cartesian coordinate system, these are called x, y, and z. A position in spacetime is called an event, and requires four numbers to be specified: the three-dimensional location in space, plus the position in time (Fig. 1). Spacetime is thus four dimensional. An event is something that happens instantaneously at a single point in spacetime, represented by a set of coordinates x, y, z and t.

The word "event" used in relativity should not be confused with the use of the word "event" in normal conversation, where it might refer to an "event" as something such as a concert, sporting event, or a battle. These are not mathematical "events" in the way the word is used in relativity, because they have finite durations and extents. Unlike the analogies used to explain events, such as firecrackers or lightning bolts, mathematical events have zero duration and represent a single point in spacetime.

The path of a particle through spacetime can be considered to be a succession of events. The series of events can be linked together to form a line which represents a particle's progress through spacetime. That line is called the particle's world line.^[4]:105

Mathematically, spacetime is a manifold, which is to say, it appears locally "flat" near each point in the same way that, at small enough scales, a globe appears flat.^[5] An extremely large scale factor, (conventionally called the speed-of-light) relates distances measured in space with distances measured in time. The magnitude of this scale factor (nearly 300,000 kilometres or 190,000 miles in space being equivalent to one second in time), along with the fact that spacetime is a manifold, implies that at ordinary, non-relativistic speeds and at ordinary, human-scale distances, there is little that humans might observe which is noticeably different from what they might observe if the world were Euclidean. It was only with the advent of sensitive scientific measurements in the mid-1800s, such as the Fizeau experiment and the Michelson–Morley experiment, that puzzling discrepancies began to be noted between observation versus predictions based on the implicit assumption of Euclidean space.^[6]

Figure 1-1. Each location in spacetime is marked by four numbers defined by a frame of reference: the position in space, and the time (which can be visualized as the reading of a clock located at each position in space). The 'observer' synchronizes the clocks according to their own reference frame.

In special relativity, an observer will, in most cases, mean a frame of reference from which a set of objects or events is being measured. This usage differs significantly from the ordinary English meaning of the term. Reference frames are inherently nonlocal constructs, and according to this usage of the term, it does not make sense to speak of an observer as having a location. In Fig. 1‑1, imagine that the frame under consideration is equipped with a dense lattice of clocks, synchronized within this reference frame, that extends indefinitely throughout the three dimensions of space. Any specific location within the lattice is not important. The latticework of clocks is used to determine the time and position of events taking place within the whole frame. The term observer refers to the entire ensemble of clocks associated with one inertial frame of reference.^[7]:17–22 In this idealized case, every point in space has a clock associated with it, and thus the clocks register each event instantly, with no time delay between an event and its recording. A real observer, however, will see a delay between the emission of a signal and its detection due to the speed of light. To synchronize the clocks, in the data reduction following an experiment, the time when a signal is received will be corrected to reflect its actual time were it to have been recorded by an idealized lattice of clocks.

In many books on special relativity, especially older ones, the word "observer" is used in the more ordinary sense of the word. It is usually clear from context which meaning has been adopted.

Physicists distinguish between what one measures or observes (after one has factored out signal propagation delays), versus what one visually sees without such corrections. Failure to understand the difference between what one measures/observes versus what one sees is the source of much error among beginning students of relativity.^[8]

History[edit]

Figure 1-2. Michelson and Morley expected that motion through the aether would cause a differential phase shift between light traversing the two arms of their apparatus. The most logical explanation of their negative result, aether dragging, was in conflict with the observation of stellar aberration.

By the mid-1800s, various experiments such as the observation of the Arago spot and differential measurements of the speed of light in air versus water were considered to have proven the wave nature of light as opposed to a corpuscular theory.^[9] Propagation of waves was then assumed to require the existence of a waving medium; in the case of light waves, this was considered to be a hypothetical luminiferous aether.^{[note 1]} However, the various attempts to establish the properties of this hypothetical medium yielded contradictory results. For example, the Fizeau experiment of 1851 demonstrated that the speed of light in flowing water was less than the sum of the speed of light in air plus the speed of the water by an amount dependent on the water's index of refraction. Among other issues, the dependence of the partial aether-dragging implied by this experiment on the index of refraction (which is dependent on wavelength) led to the unpalatable conclusion that aether simultaneously flows at different speeds for different colors of light.^[10] The famous Michelson–Morley experiment of 1887 (Fig. 1‑2) showed no differential influence of Earth's motions through the hypothetical aether on the speed of light, and the most likely explanation, complete aether dragging, was in conflict with the observation of stellar aberration.^[6]

George Francis FitzGerald in 1889, and Hendrik Lorentz in 1892, independently proposed that material bodies traveling through the fixed aether were physically affected by their passage, contracting in the direction of motion by an amount that was exactly what was necessary to explain the negative results of the Michelson–Morley experiment. (No length changes occur in directions transverse to the direction of motion.)

By 1904, Lorentz had expanded his theory such that he had arrived at equations formally identical with those that Einstein were to derive later (i.e. the Lorentz transform), but with a fundamentally different interpretation. As a theory of dynamics (the study of forces and torques and their effect on motion), his theory assumed actual physical deformations of the physical constituents of matter.^{[11]:163–174} Lorentz's equations predicted a quantity that he called local time, with which he could explain the aberration of light, the Fizeau experiment and other phenomena. However, Lorentz considered local time to be only an auxiliary mathematical tool, a trick as it were, to simplify the transformation from one system into another.

Other physicists and mathematicians at the turn of the century came close to arriving at what is currently known as spacetime. Einstein himself noted, that with so many people unraveling separate pieces of the puzzle, "the special theory of relativity, if we regard its development in retrospect, was ripe for discovery in 1905."^[12]

An important example is Henri Poincaré,^{[13][14]:73–80,93–95} who in 1898 argued that the simultaneity of two events is a matter of convention.^{[15][note 2]} In 1900, he recognized that Lorentz's "local time" is actually what is indicated by moving clocks by applying an explicitly operational definition of clock synchronization assuming constant light speed.^{[note 3]} In 1900 and 1904, he suggested the inherent undetectability of the aether by emphasizing the validity of what he called the principle of relativity, and in 1905/1906^[16] he mathematically perfected Lorentz's theory of electrons in order to bring it into accordance with the postulate of relativity. While discussing various hypotheses on Lorentz invariant gravitation, he introduced the innovative concept of a 4-dimensional spacetime by defining various four vectors, namely four-position, four-velocity, and four-force.^[17][18] He did not pursue the 4-dimensional formalism in subsequent papers, however, stating that this line of research seemed to "entail great pain for limited profit", ultimately concluding "that three-dimensional language seems the best suited to the description of our world".^[18] Furthermore, even as late as 1909, Poincaré continued to believe in the dynamical interpretation of the Lorentz transform.^{[11]:163–174} For these and other reasons, most historians of science argue that Poincaré did not invent what is now called special relativity.^[14][11]

In 1905, Einstein introduced special relativity (even though without using the techniques of the spacetime formalism) in its modern understanding as a theory of space and time.^[14][11] While his results are mathematically equivalent to those of Lorentz and Poincaré, Einstein showed that the Lorentz transformations are not the result of interactions between matter and aether, but rather concern the nature of space and time itself. He obtained all of his results by recognizing that the entire theory can be built upon two postulates: The principle of relativity and the principle of the constancy of light speed.

Einstein performed his analysis in terms of kinematics (the study of moving bodies without reference to forces) rather than dynamics. His work introducing the subject was filled with vivid imagery involving the exchange of light signals between clocks in motion, careful measurements of the lengths of moving rods, and other such examples.^{[19][note 4]}

In addition, Einstein in 1905 superseded previous attempts of an electromagnetic mass–energy relation by introducing the general equivalence of mass and energy, which was instrumental for his subsequent formulation of the equivalence principle in 1907, which declares the equivalence of inertial and gravitational mass. By using the mass–energy equivalence, Einstein showed, in addition, that the gravitational mass of a body is proportional to its energy content, which was one of early results in developing general relativity. While it would appear that he did not at first think geometrically about spacetime,^[21]:219 in the further development of general relativity Einstein fully incorporated the spacetime formalism.

When Einstein published in 1905, another of his competitors, his former mathematics professor Hermann Minkowski, had also arrived at most of the basic elements of special relativity. Max Born recounted a meeting he had made with Minkowski, seeking to be Minkowski's student/collaborator:^[22]

I went to Cologne, met Minkowski and heard his celebrated lecture 'Space and Time' delivered on 2 September 1908. […] He told me later that it came to him as a great shock when Einstein published his paper in which the equivalence of the different local times of observers moving relative to each other was pronounced; for he had reached the same conclusions independently but did not publish them because he wished first to work out the mathematical structure in all its splendor. He never made a priority claim and always gave Einstein his full share in the great discovery.

Minkowski had been concerned with the state of electrodynamics after Michelson's disruptive experiments at least since the summer of 1905, when Minkowski and David Hilbert led an advanced seminar attended by notable physicists of the time to study the papers of Lorentz, Poincaré et al. However, it is not at all clear when Minkowski began to formulate the geometric formulation of special relativity that was to bear his name, or to which extent he was influenced by Poincaré's four-dimensional interpretation of the Lorentz transformation. Nor is it clear if he ever fully appreciated Einstein's critical contribution to the understanding of the Lorentz transformations, thinking of Einstein's work as being an extension of Lorentz's work.^[23]

Figure 1-4. Hand-colored transparency presented by Minkowski in his 1908 Raum und Zeit lecture

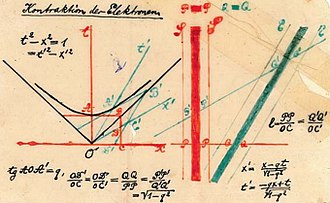
On 5 November 1907 (a little more than a year before his death), Minkowski introduced his geometric interpretation of spacetime in a lecture to the Göttingen Mathematical society with the title, The Relativity Principle (Das Relativitätsprinzip).^{[note 5]} On 21 September 1908, Minkowski presented his famous talk, Space and Time (Raum und Zeit),^[24] to the German Society of Scientists and Physicians. The opening words of Space and Time include Minkowski's famous statement that "Henceforth, space for itself, and time for itself shall completely reduce to a mere shadow, and only some sort of union of the two shall preserve independence." Space and Time included the first public presentation of spacetime diagrams (Fig. 1‑4), and included a remarkable demonstration that the concept of the invariant interval (discussed below), along with the empirical observation that the speed of light is finite, allows derivation of the entirety of special relativity.^{[note 6]}

The spacetime concept and the Lorentz group are closely connected to certain types of sphere, hyperbolic, or conformal geometries and their transformation groups already developed in the 19th century, in which invariant intervals analogous to the spacetime interval are used.^{[note 7]}

Einstein, for his part, was initially dismissive of Minkowski's geometric interpretation of special relativity, regarding it as überflüssige Gelehrsamkeit (superfluous learnedness). However, in order to complete his search for general relativity that started in 1907, the geometric interpretation of relativity proved to be vital, and in 1916, Einstein fully acknowledged his indebtedness to Minkowski, whose interpretation greatly facilitated the transition to general relativity.^{[11]:151–152} Since there are other types of spacetime, such as the curved spacetime of general relativity, the spacetime of special relativity is today known as Minkowski spacetime.

Spacetime in special relativity[edit]

Spacetime interval[edit]

In three dimensions, the distance between two points can be defined using the Pythagorean theorem:

Although two viewers may measure the x, y, and z position of the two points using different coordinate systems, the distance between the points will be the same for both (assuming that they are measuring using the same units). The distance is "invariant".

In special relativity, however, the distance between two points is no longer the same if measured by two different observers when one of the observers is moving, because of Lorentz contraction. The situation is even more complicated if the two points are separated in time as well as in space. For example, if one observer sees two events occur at the same place, but at different times, a person moving with respect to the first observer will see the two events occurring at different places, because (from their point of view) they are stationary, and the position of the event is receding or approaching. Thus, a different measure must be used to measure the effective "distance" between two events.

In four-dimensional spacetime, the analog to distance is the interval. Although time comes in as a fourth dimension, it is treated differently than the spatial dimensions. Minkowski space hence differs in important respects from four-dimensional Euclidean space. The fundamental reason for merging space and time into spacetime is that space and time are separately not invariant, which is to say that, under the proper conditions, different observers will disagree on the length of time between two events (because of time dilation) or the distance between the two events (because of length contraction). But special relativity provides a new invariant, called the spacetime interval, which combines distances in space and in time. All observers who measure time and distance carefully will find the same spacetime interval between any two events. Suppose an observer measures two events as being separated in time by and a spatial distance Then the spacetime interval between the two events that are separated by a distance in space and by in the -coordinate is:

or for three space dimensions,

^[28]

The constant the speed of light, converts the units used to measure time (seconds) into units used to measure distance (meters).

Although for brevity, one frequently sees interval expressions expressed without deltas, including in most of the following discussion, it should be understood that in general, means , etc. We are always concerned with differences of spatial or temporal coordinate values belonging to two events, and since there is no preferred origin, single coordinate values have no essential meaning.

Figure 2-1. Spacetime diagram illustrating two photons, A and B, originating at the same event, and a slower-than-light-speed object, C

The equation above is similar to the Pythagorean theorem, except with a minus sign between the and the terms. The spacetime interval is the quantity not itself. The reason is that unlike distances in Euclidean geometry, intervals in Minkowski spacetime can be negative. Rather than deal with square roots of negative numbers, physicists customarily regard as a distinct symbol in itself, rather than the square of something.^[21]:217

Because of the minus sign, the spacetime interval between two distinct events can be zero. If is positive, the spacetime interval is timelike, meaning that two events are separated by more time than space. If is negative, the spacetime interval is spacelike, meaning that two events are separated by more space than time. Spacetime intervals are zero when In other words, the spacetime interval between two events on the world line of something moving at the speed of light is zero. Such an interval is termed lightlike or null. A photon arriving in our eye from a distant star will not have aged, despite having (from our perspective) spent years in its passage.

A spacetime diagram is typically drawn with only a single space and a single time coordinate. Fig. 2‑1 presents a spacetime diagram illustrating the world lines (i.e. paths in spacetime) of two photons, A and B, originating from the same event and going in opposite directions. In addition, C illustrates the world line of a slower-than-light-speed object. The vertical time coordinate is scaled by so that it has the same units (meters) as the horizontal space coordinate. Since photons travel at the speed of light, their world lines have a slope of ±1. In other words, every meter that a photon travels to the left or right requires approximately 3.3 nanoseconds of time.

There are two sign conventions in use in the relativity literature:

and

These sign conventions are associated with the metric signatures(+ − − −) and (− + + +). A minor variation is to place the time coordinate last rather than first. Both conventions are widely used within the field of study.

Reference frames[edit]

Figure 2-2. Galilean diagram of two frames of reference in standard configuration

Figure 2-3. (a) Galilean diagram of two frames of reference in standard configuration, (b) spacetime diagram of two frames of reference, (c) spacetime diagram showing the path of a reflected light pulse

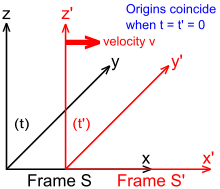
To gain insight in how spacetime coordinates measured by observers in different reference frames compare with each other, it is useful to work with a simplified setup with frames in a standard configuration. With care, this allows simplification of the math with no loss of generality in the conclusions that are reached. In Fig. 2‑2, two Galilean reference frames (i.e. conventional 3-space frames) are displayed in relative motion. Frame S belongs to a first observer O, and frame S′ (pronounced "S prime") belongs to a second observer O′.

• The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
• Frame S′ moves in the x-direction of frame S with a constant velocity v as measured in frame S.
• The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.^[4]:107

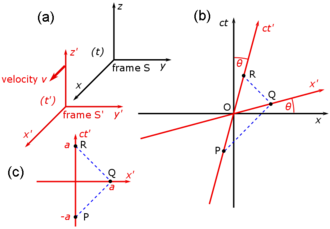
Fig. 2‑3a redraws Fig. 2‑2 in a different orientation. Fig. 2‑3b illustrates a spacetime diagram from the viewpoint of observer O. Since S and S′ are in standard configuration, their origins coincide at times t = 0 in frame S and t′ = 0 in frame S′. The ct′ axis passes through the events in frame S′ which have x′ = 0. But the points with x′ = 0 are moving in the x-direction of frame S with velocity v, so that they are not coincident with the ct axis at any time other than zero. Therefore, the ct′ axis is tilted with respect to the ct axis by an angle θ given by

The x′ axis is also tilted with respect to the x axis. To determine the angle of this tilt, we recall that the slope of the world line of a light pulse is always ±1. Fig. 2‑3c presents a spacetime diagram from the viewpoint of observer O′. Event P represents the emission of a light pulse at x′ = 0, ct′ = −a. The pulse is reflected from a mirror situated a distance a from the light source (event Q), and returns to the light source at x′ = 0, ct′ = a (event R).

The same events P, Q, R are plotted in Fig. 2‑3b in the frame of observer O. The light paths have slopes = 1 and −1, so that △PQR forms a right triangle with PQ and QR both at 45 degrees to the x and ct axes. Since OP = OQ = OR, the angle between x′ and x must also be θ.^{[4]:113–118}

While the rest frame has space and time axes that meet at right angles, the moving frame is drawn with axes that meet at an acute angle. The frames are actually equivalent. The asymmetry is due to unavoidable distortions in how spacetime coordinates can map onto a Cartesian plane, and should be considered no stranger than the manner in which, on a Mercator projection of the Earth, the relative sizes of land masses near the poles (Greenland and Antarctica) are highly exaggerated relative to land masses near the Equator.

Light cone[edit]

Figure 2-4. The light cone centered on an event divides the rest of spacetime into the future, the past, and "elsewhere"

In Fig. 2-4, event O is at the origin of a spacetime diagram, and the two diagonal lines represent all events that have zero spacetime interval with respect to the origin event. These two lines form what is called the light cone of the event O, since adding a second spatial dimension (Fig. 2‑5) makes the appearance that of two right circular cones meeting with their apices at O. One cone extends into the future (t>0), the other into the past (t<0).

Figure 2-5. Light cone in 2D space plus a time dimension

A light (double) cone divides spacetime into separate regions with respect to its apex. The interior of the future light cone consists of all events that are separated from the apex by more time (temporal distance) than necessary to cross their spatial distance at lightspeed; these events comprise the timelike future of the event O. Likewise, the timelike past comprises the interior events of the past light cone. So in timelike intervals Δct is greater than Δx, making timelike intervals positive. The region exterior to the light cone consists of events that are separated from the event O by more space than can be crossed at lightspeed in the given time. These events comprise the so-called spacelike region of the event O, denoted "Elsewhere" in Fig. 2‑4. Events on the light cone itself are said to be lightlike (or null separated) from O. Because of the invariance of the spacetime interval, all observers will assign the same light cone to any given event, and thus will agree on this division of spacetime.^[21]:220

The light cone has an essential role within the concept of causality. It is possible for a not-faster-than-light-speed signal to travel from the position and time of O to the position and time of D (Fig. 2‑4). It is hence possible for event O to have a causal influence on event D. The future light cone contains all the events that could be causally influenced by O. Likewise, it is possible for a not-faster-than-light-speed signal to travel from the position and time of A, to the position and time of O. The past light cone contains all the events that could have a causal influence on O. In contrast, assuming that signals cannot travel faster than the speed of light, any event, like e.g. B or C, in the spacelike region (Elsewhere), cannot either affect event O, nor can they be affected by event O employing such signalling. Under this assumption any causal relationship between event O and any events in the spacelike region of a light cone is excluded.^[29]

Relativity of simultaneity[edit]

Figure 2-6. Animation illustrating relativity of simultaneity

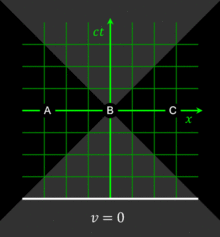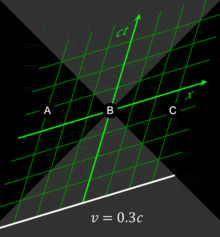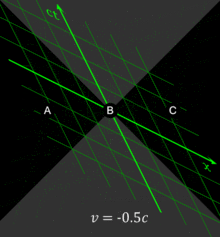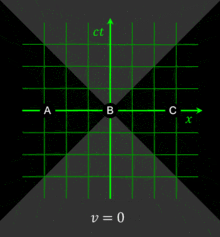
All observers will agree that for any given event, an event within the given event's future light cone occurs after the given event. Likewise, for any given event, an event within the given event's past light cone occurs before the given event. The before–after relationship observed for timelike-separated events remains unchanged no matter what the reference frame of the observer, i.e. no matter how the observer may be moving. The situation is quite different for spacelike-separated events. Fig. 2‑4